Simulating stable marriage algorithms

A larger dating pool doesn't help much.

The code for this post can be found here.

A long time ago, I toyed with some ideas for matchmaking algorithms. With the help of ChatGPT, I ran a few simulations of one of those algorithms, Gayle-Shapely.

Gayle-Shapely is a “stable marriage algorithm”, it starts with two groups of people¹, suitors that approach potential dates, and reviewers, who make choices between different suitors. It assumes that each person has a ranking of all potential partners and sticks to it. If that’s the case, Gayle-Shapely will find a stable matching, one where no pair of people would prefer to run off with each other rather than stay with their partners. Everyone is matched with the highest-ranked partner they can get.

These algorithms have been used to match doctors to residency, but as far as I know, nobody has actually used them to pair up couples. Would it work²?

Creating partner rankings

We need some algorithm to assign each player a ranking over potential partners. Ideally, this algorithm has a tunable noise parameter so that members of the same group can have either highly correlated or highly uncorrelated rankings.

The solution I came up with is to have everyone start with identical “utilities” for each partner, and then add a random component to each utility so that individuals differ from each other. If the variance of the noise is zero, everyone will have the same ranking, if the variance is small, rankings will be correlated, and if the variance is very high the rankings will be random for each person.

Simulating matchmaking rounds

To simulate a matchmaking round, I run the Gayle-Shapely algorithm given the suitor and reviewer preferences.

We want to know how good of a partner everyone ends up with, so to compare across different dating pools, let’s track the percentile of partner people end up with (according to their own ranking). By repeating the matchmaking simulation many times, we can get good statistics and compare a bunch of different pool sizes.

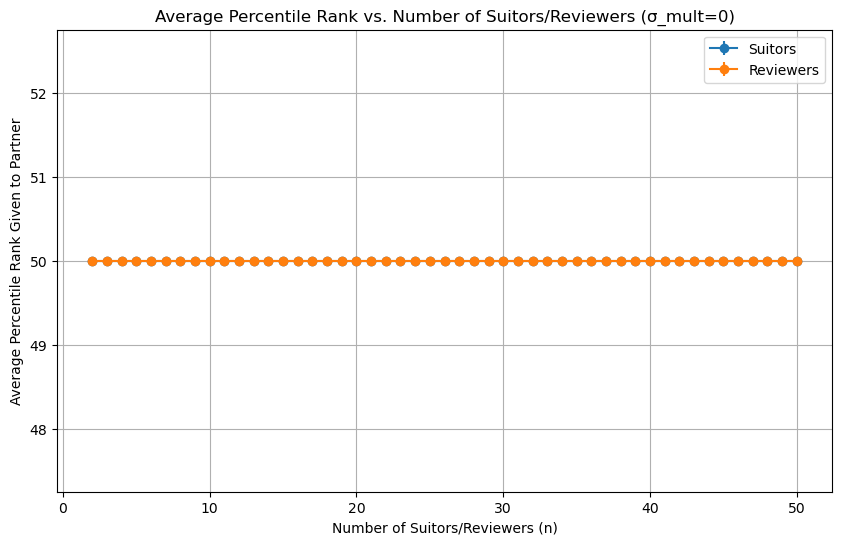
First, as a sanity check, we can simulate a round where all the suitors and reviewers have the same preferences:

Makes sense, the average person should end up with the 50th percentile partner.

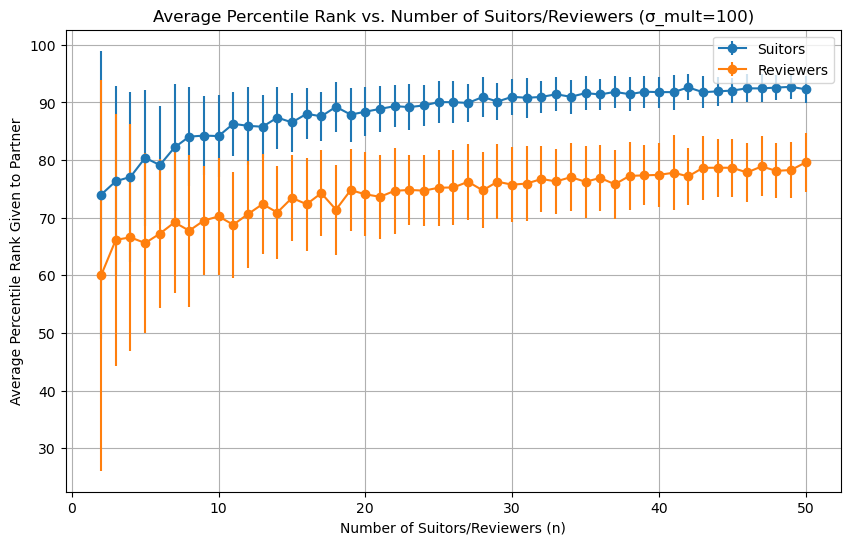
Now let’s assume everyone has completely random preferences over the set of potential partners. We can simulate this by setting the variance of the noise very high.

I ran the simulation 100 times for different dating pool sizes and got this:

So as a proposer, your average partner is around 90th percentile even with a pool of 20 potential dates. The situation is worse for reviewers, they get someone who’s about 75th percentile. Things get better for everyone with more options, with a 50-person dating pool, suitors can expect a 93rd percentile partner, while reviewers top out under the 80th percentile. Those aren’t terrible to pick someone for a first date, but I would like something much higher for an algorithm choosing a spouse, especially if I’m a reviewer³.

But peoples rankings of other partners aren’t random, there’s a lot of correlation! Some people are just plain hotter than others.

Do you doubt that some people are hotter than others?

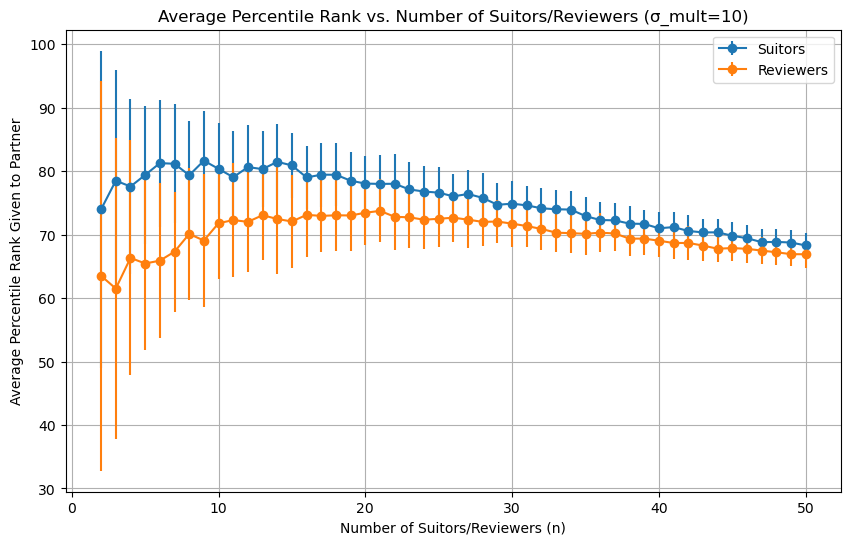
With correlated rankings, increasing the size of the dating pool increases partner quality a little before it starts to fall off:

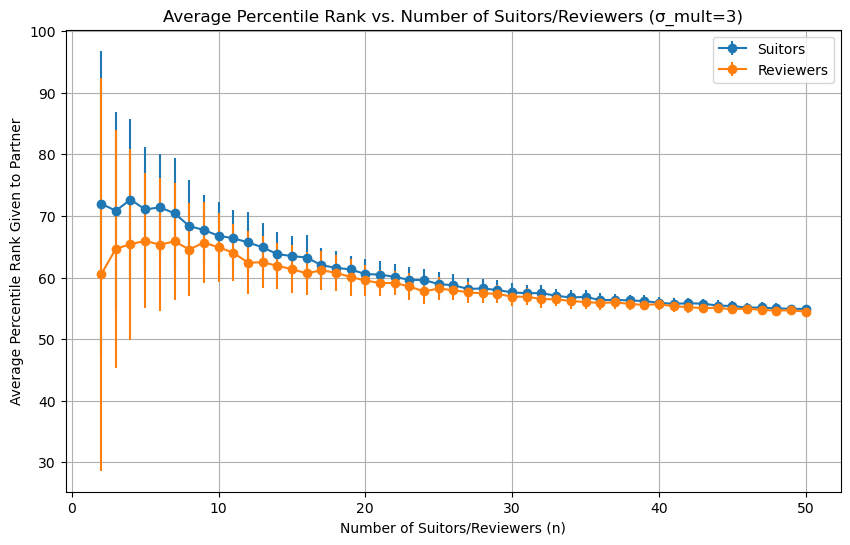
It seems like the more uncorrelated peoples preferences, the better. With less correlated preferences we see an improvement with larger dating pools, but as preferences get more correlated, everything converges towards the flat line associated with identical preferences. We can see that by setting the variance pretty low:

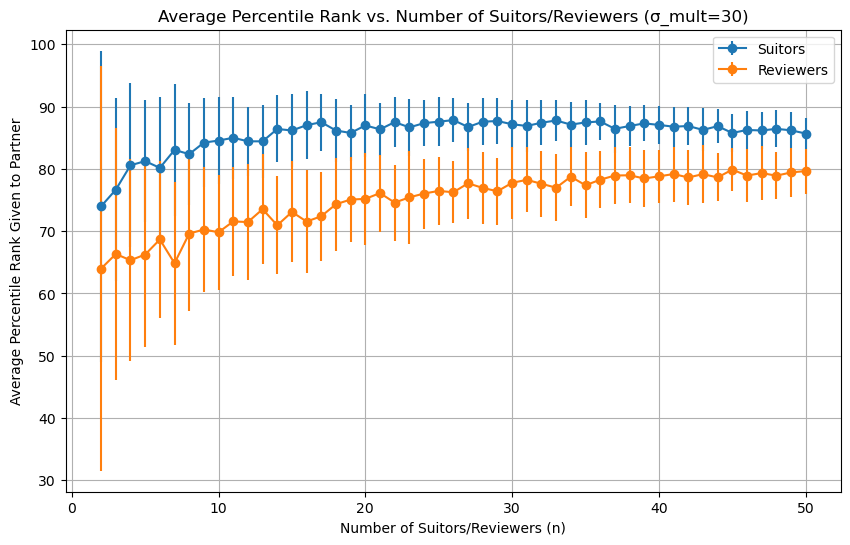
For completeness sake, we can set the variance very high (sigma_mult=30), which should produce a situation similar to random preferences (sigma_mult=100):

Conclusion

My takeaway here is that moving to much larger dating pools doesn’t help much in terms of the quality of the partner you end up with. When people have totally random preferences, partner percentile has diminishing returns past a dating pool of around 30⁴⁵.

But when there’s a little correlation, average partner quality actually goes down at higher number of suitors. 15 options seems like the sweet spot here. That makes it more important to create small pools of mutually interested people, perhaps around a shared social group or hobby.

The partner quality you end up with isn’t that high. For a pool of 15 people, suitors end up with someone they ranked 3rd on average, and reviewers end up with someone they ranked 5th (for sigma_mult=10). Not that great if you’re choosing a life partner, but I think it’s passable for a first date. Remember, in the real world, people’s first impressions (especially at the top) will be pretty noisy, so going from a 90th percentile first impression to a 99th percentile first impression won’t actually translate to a better first date. From this perspective, a system that pairs you up with one of your top 5 choices isn’t so bad.

But there’s a bigger problem that Gayle-Shapely can’t address. Though it can pair you up with a relatively-good partner in the pool, it does nothing to guarantee that the pool has people you want to date.

Dating markets have this problem where people pair off and drop out of the pool, leaving behind a subset of people who (on average) have trouble forming lasting relationships. Matchmaking in the later pools is a double-edged sword.

I can’t tell if this is solvable. What would we do, force the relationship stabilizers to be with the destabilizers? Love is a free-for-all, I doubt people would go along with arranged marriages. Perhaps the best we can do is warn people of the consequences of waiting too long.

Finally, some ideas to extend these simulations:

• I didn’t even bother to look at the histograms for partner percentile. Are there two groups of people ending up with good versus bad partners?

• Infer a beta distribution for each point rather than showing the variance

• How much benefit do you get from being a top-ranked partner? In other words, how does partner quality increase as a players non-random component of attractiveness increase?

• Make a more complete model of the dating market, including multiple rounds of Gayle-Shapely and couples that drop out of the pool for a period of time.

• A more sophisticated model of dating is an optimal stopping problem similar to a “Pandora’s box problem”: you have an initial evaluation of someone, date them to learn more, and then decide whether to learn more about them or meet other people.

• Can we extend this model to groups to model the formation of friend groups?

• Perhaps the model from Thickness and Information in Dynamic Matching Markets is a good way to extend this analysis.

1. The original formulation of the problem is heteronormative, but that doesn’t need to be the case here. For example, a matchmaking service for gay men could just randomly assign people to the suitor or reviewer group.

2. There’s a couple things you have to do to make this work in the real world. A big problem is people dropping out if their partner isn’t good enough. See the original post for more discussion.

3. For pairing heterosexual couples, it’s probably better for women to be the suitors since downsides of bad partner are higher.

4. This can be a little deceptive, going from a 90th to a 99th percentile partner is much better than going from 50th to 59th percentile partner even though both are only a 9 point improvement.

5. Regardless, The gains from larger dating pools probably aren’t achievable in practice, imagine how long it would take to decide how to rank 100 people! In that case, you’d probably have to use AI tools to set the rankings.