Authors: Sam Harsimony & Victor Sint Nicolaas
Introduction
Public goods are an important concept from economics. Once introduced to the idea that some resources can be accessible to anyone in infinite supply, you start to see them everywhere. Public parks, art, and ideas, are some natural examples of public goods. Formally, they’re defined as goods that are both nonexcludable (it’s infeasible to prevent someone from consuming the good) and nonrivalrous (one person’s consumption can not reduce another person’s consumption of the good).
Beyond the existing examples, consider that today’s technology is making some private goods closely resemble public goods. For instance, online entertainment, 3D printed parts, RNA vaccines, and software can be represented as digital information, a resource that is naturally nonrivalrous and nonexcludable. It may be fruitful to consider how to produce these commodities as public goods.
In addition, as the world economy becomes more interconnected, more domains of life begin to resemble public goods. Nowadays, trade policy in one country can affect the economy of many others, necessitating a global approach. Air quality, water pollution, and land management involve coordination problems due to the scale of human resource use. Now more than ever, we need to think carefully about how to provide public goods on a global scale.
The fact that public goods are not excludable creates a “free-rider problem”, where people are incentivized to enjoy the benefits of the good without paying for it. What’s the point of contributing to a public park if non-contributors can use it too? It’s well established that even in groups of rational actors, public goods are typically underfunded. If we want to see more science funding, open-source software, and environmental cleanup, we need to find some way to gather support.
A lot of research has focused on designing mechanisms to solve the free-rider problem and get individuals to collectively fund public goods. But this work quickly ran into an impossibility theorem that no mechanism can simultaneously achieve four desirable criteria:
Pareto Efficiency: The outcome achieved by the mechanism maximizes the overall welfare or some other desirable objective function.
Incentive Compatibility: Designing mechanisms so that participants are motivated to act truthfully, without gaining by misrepresenting their preferences.
Individual Rationality: Ensuring that every participant has a non-negative utility (or at least no worse off) by participating in the mechanism.
Budget Balance: The mechanism generates sufficient revenue to cover its costs or payouts, without running a net deficit.
Subsequent research has focused on mechanisms that lack one of these four properties, but possess other desirable characteristics such as coalition-proofness, approximate budget balance, or approximate efficiency.
This report will mostly focus on mechanisms that use subsidies to remove the budget constraint, but other combinations of properties have been studied. For example, Faltings details a mechanism which only achieves approximate efficiency, but possesses incentive compatibility, individual rationality, and budget-balance. Kuzmics and Steg characterize threshold mechanisms that are incentive compatible, individually rational, and budget balanced (with an additional condition). Kunimoto and Zhang provide a more general characterization of mechanisms lacking efficiency. Mechanisms that lack incentive compatibility are rare, but often a weaker form of incentive compatibility known as Bayes-Nash incentive compatibility is used to study public goods funding. Mechanisms that lack individual rationality (sometimes maligned as coercive or extortive mechanisms) are rarely analyzed in the literature (with some exceptions), but are common in the real world; taxes are one example of such a funding system.
Some Solutions to the Public Goods funding problem
Assurance Contracts
First proposed by Bagnoli and Lipman, assurance contracts have a simple and intuitive appeal. Each funder agrees to spend a certain amount towards a public good conditional on the total funding being sufficient to produce the good. If not everyone agrees to the terms, then no money is spent on the project. Donors can feel assured that their money will only be spent if there is sufficient support for the public good. Assurance contracts work particularly well with smaller groups of easily identifiable participants, especially when the game can be repeated.
Several crowdfunding platforms such as Kickstarter and IndieGoGo have used assurance contracts to support various projects (though not all of them are public goods). Kickstarter alone has directed almost $7 billion to such projects to date.
Assurance contracts can be used for non-monetary coordination as well, for example, Free State Project obtained mutual commitments for 20,000 individuals to move to New Hampshire in a bid to influence the politics of the state.
Though assurance contracts have a “threshold reached” Nash equilibrium, they also have an equilibrium where nobody pays. Observe that in the simplified payoff matrix below both “Do Not Contribute/Do Not Contribute” and “Contribute / Contribute“ are Nash equilibria. Either is possible in a real-world setting. If there are additional costs of time or effort to participate in the contract, then the no-pay equilibrium may be favored.
Example payoff matrix for the assurance game (link)
To resolve this issue, Alex Tabarrok suggested a modification called Dominant Assurance Contracts where the mechanism designer gives every contributor a refund bonus if the contract fails. For example, in addition to returning their contributions, the mechanism designer might give all contributors an additional $5 if the total donations aren’t sufficient to support the project.
If there’s a chance that the contract will fail, a refund bonus incentivizes people to participate in the mechanism, making the all-pay equilibrium more likely. This comes with the drawback that the mechanism designer must pay the participants in some cases (e.g. when the contract fails), which is a common theme.
Zubrickas proposed a simple modification of dominant assurance contracts where people are given a refund bonus proportional to the amount they offered to donate, this incentivizes larger contributions than the fixed refund from Tabarrok’s original proposal.
There have been many variations on the idea of conditional donations towards a public good. For example, the Conditional Contributions Mechanism allows donors to make variable sized commitments to fund the project conditional on the total amount committed. Similarly, the Binary Conditional Contributions Mechanism allows users to condition their donation on the number of unique funders. Extensions such as the Street Performer Protocol consider time-limited spending commitments.
Vickrey-Clarke-Groves Mechanism
Vickrey-Clarke-Groves (VCG) mechanisms are one of the best studied procedures for funding public goods. VGC encompasses a wide class of similar mechanisms, but most work focuses on the Clarke Pivot Rule which ensures that all individuals pay into the public good and that the mechanism is individually rational.
The VCG mechanism works by asking individuals for a utility function at every funding level of the public good and selects a funding level that maximizes the sum of their utilities. Each individual is then charged according to:
Where x is the amount an individual donates to the project and x is the optimal total amount of funding for the good. vi is the utility function of individual i, it corresponds to the utility an individual receives when the total funding for the public good is x.
The main issue with the VCG mechanism is that it requires a very large amount of information from each user. Participants may not have a detailed sense of their utility function with respect to different funding levels. Compare this with other mechanisms that only require users to provide a single contribution amount. This, among other reasons, has prevented the use of VCG mechanisms in practice. However, it is still possible that VCG mechanisms could be adopted among a set of sophisticated actors.
Quadratic Funding
Quadratic funding (QF) is one of the newest innovations in public goods funding mechanisms. A quadratic approach to voting was first proposed by Glen Weyl, Eric Posner, and Steven Lalley. This idea was later turned into a mechanism for public goods funding by Buterin, Hitzig, and Weyl and is now referred to as quadratic funding.
The total contribution to the public good is simply the sum of the square roots of individual contributions:
Each individual donates their stated amount, and the mechanism designer pays for the difference between the sum of the ci’s and copt. It can be proved that there is always a deficit that the mechanism designer must pay.
Quadratic funding has a close theoretical link with the VCG mechanism, and like VCG, it requires a subsidy in order to induce incentive compatibility and efficiency. Both mechanisms also fall prone to collusion between players and sybil attacks.
One technique to reduce collusion is to identify groups of contributors that will likely coordinate and lower the subsidy going to their preferred causes. Pairwise discounting quadratic funding is one example of this.
Quadratic funding benefits from an enthusiastic and sophisticated community centered around Gitcoin grants. Gitcoin grants will continue to be an important source of on-the-ground innovation in quadratic funding.
Lotteries
Lotteries have historically been used as a means to finance public goods. Morgan initiated the first formal study of lotteries as a public goods funding mechanism. Since then, lotteries have undergone extensive theoretical and experimental research. Combined with their historical success, lotteries are a promising crowdfunding mechanism.
They work by using an external source of funding to provide a lottery prize. Individual “donors” buy lottery tickets for a chance to receive the cash prize, knowing that ticket sales will be spent towards the public good. A winner is selected randomly from one of the tickets and the winner receives the entire lottery prize. All lottery proceeds from ticket sales are spent towards the public good.
Like the other mechanisms, this approach requires subsidies in the form of a lottery prize in order to function. It can be shown that altruistic donors can generate more funding for the good by donating towards the lottery prize rather than buying tickets directly.
Lotteries are approximately efficient public goods funding mechanisms and the level of funding approaches the optimal level as the prize grows. However, in the limit of large populations, contributions from the lottery mechanism converge to that of voluntary contributions and should fall to zero.
Some extensions have been proposed. Apinunmahakul and Barham have shown that charging an additional fee to participate in the lottery can increase the total contributions. Lange considered a mechanism where a few donors coordinate to provide the lottery prize, which can substantially increase the total funding for the good. Villalba et. al. propose a more sophisticated “hybrid lottery” which they claim is self-financing.
Lindahl Process
The Lindahl mechanism was one of the first proposed models of public goods funding. Here, the mechanism designer asks each individual for their marginal willingness to pay for a public good at various sizes and then adds up the individual curves to get the aggregate marginal willingness-to-pay (WTP).
Next, they find the point where the marginal cost of providing the public good intersects the aggregate marginal WTP curve. This is the highest budget for the public good that is still worthwhile for the participants, so the public good is given that amount of funding. Finally, each individual is charged based on their stated WTP.
The Lindahl process is not strategyproof, so individuals tend to under-report their valuations. Additionally, the mechanism requires users to provide detailed information about their preferences, which may be impractical.
The more recently proposed S-process has some similarities to Lindahl’s original idea, where donors iteratively reveal their willingness to pay for the next marginal unit of a public good.
Indicators of Mechanism Success
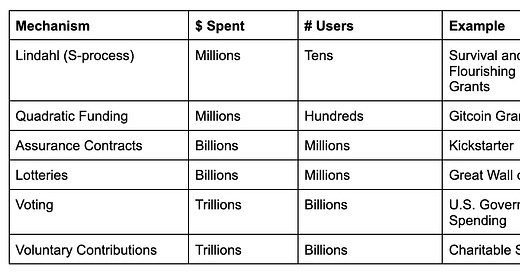
Beyond theoretical research, it’s important to assess how successful a mechanism is in reality. Ultimately, a mechanism is valuable if it enables public goods that would not otherwise have been funded. This is hard to measure in practice, so a number of proxies may be considered such as the number of users, the total amount of money spent, and the number of successful funding rounds.
Only a few mechanisms have been used outside the lab. Assurance contracts, lotteries, and quadratic funding have all been employed to various degrees. However, today, the majority of public goods funding today comes from either government spending or charitable donations. For this reason, we include “voting” and “voluntary contributions” in the table to represent government spending and charitable donations respectively.
Because these mechanisms are employed in different communities under different constraints, it can be difficult to make a clear comparison of mechanism success. The public goods literature has a history of testing mechanisms under controlled conditions with a handful of participants. While these results are unlikely to generalize to the real world, they provide a clean comparison of different mechanisms and can be used to rule out mechanisms that perform poorly even under ideal conditions. This literature is extensive and not easily summarized, but a list of relevant papers is included in the appendix.
Privacy and Decentralization in Public Goods Funding Mechanisms
Much of the mechanism design literature began before the advent of cryptocurrency, zero-knowledge proofs, and other cryptographic innovations. It’s natural to wonder how these primitives can improve public goods funding.
Typically, mechanism design assumes the existence of a trusted 3rd party who collects information from participants and calculates individual payments to the public good. However, this assumption is often unrealistic.
Requiring users to send information to a third party reduces privacy, which adds a cost that can reduce participation. Worse, an untrustworthy third party adds several sources of risk. For example, they may compute payments incorrectly or collude with other participants. If the 3rd party receives some surplus of payments from the process, their commitment to an effective mechanism may not be credible. Fortunately, recent developments in cryptography make it possible to constrain the 3rd party or remove them entirely.
Some applications of cryptography to public goods funding
Below, we highlight how generically programmable tools from cryptography can improve mechanism design.
The Default
This is the standard case considered in mechanism design literature. Cryptographic techniques have to improve upon this scenario in order to justify the increased cost and complexity.
Procedure: Some (possibly untrusted) 3rd party accepts spending commitments from users, computes the funding levels for each public good, and bills users accordingly.
Privacy: The 3rd party learns user preferences. Users learn only the total amount they spent and potentially the funding levels for each public good. Users have no way to verify that funding levels were computed correctly.
Zero-Knowledge Proofs
Procedure: A 3rd party collects all user’s spending commitments and computes the funding levels for each public good. The 3rd party then provides a zero-knowledge proof that the funding levels were computed correctly. Additional techniques such as re-randomizable encryption allow users to anonymize their contributions.
Privacy: The 3rd party may learn no user preferences. Users learn only the total amount they spent and potentially the funding levels for each public good. Users can verify that the funding levels were computed correctly.
Fully Homomorphic Encryption
Procedure: Users encrypt their set of spending commitments and delegate a 3rd party to compute funding levels (possibly with a proof of correctness).
Privacy: Users may learn other users' spending commitments while computing the encryption. This may be avoided by employing multi-party computation. Users learn the funding levels for each public good. The 3rd party learns nothing. Users may not know that funding levels were computed correctly unless the 3rd party is asked to provide a proof of this fact.
Since FHE requires users to perform some multiparty computation before communicating with the third party, it is unlikely that FHE provides an advantage over MPC. This is especially true when the funding mechanism is easy to compute and 3rd party computational power is not needed.
Multi-Party Computation
Setup: Users compute funding levels for each project using multiparty computation. The process outputs the total amount each user must spend and the funding levels for each good. Alternatively, the MPC setup can be adjusted so that users only learn their own spending.
Privacy: The total amount each user must spend becomes public. Alternative formulations may hide this information. Additional steps can be taken to verify the correctness of the output.
Cryptocurrency and Smart Contracts
The details of processing payments can be critical to ensuring the privacy of a mechanism. Additionally, censorship from established financial institutions may add significant risk, reducing mechanism effectiveness.
Censorship from payment processors is surprisingly common. In February of 2023, Stripe told Manifold Markets that it would stop processing payments unless Manifold eliminated their charitable donations program due to superficial similarities to gambling. This was particularly surprising given Stripe’s charitable mission and values. Though Manifold successfully appealed the decision, there is still risk that Stripe may ask them to shut down the charitable fund in the future.
Given this and other examples, it’s valuable for public goods funding mechanisms to implement payments in a decentralized manner. Cryptocurrency and smart contracts can be used to collect and disburse payments removing risks associated with 3rd party payment processors. Of course, this must be balanced with the cost and complexity of using cryptocurrency.
Trusted Execution Environments
Trusted Execution Environments (TEE’s) can be used in place of a 3rd party for computing funding allocations, exchanging trust in the 3rd party for trust in the security of the hardware. TEE’s can publish a hash of the software they’re running so that users can verify that the correct program is being executed. With this setup participants can simply send their funding commitments to the TEE directly. The TEE may also be used to process payments. Unfortunately, TEE’s experience regular security breaches so they cannot be relied on entirely to provide privacy.
The Drawbacks of Decentralization and Privacy
While decentralization and privacy provide benefits to participants, they do have trade offs. In general, decentralized mechanisms require more communication between participants, larger amounts of computation, and are more complicated relative to their centralized counterparts. The benefits of removing a third party may not always outweigh these costs.
Many mechanisms benefit from the public nature of users’ contributions. The reputation effects of donating to a public good can increase the incentive to give, and in a repeated game, observing players actions is critical for punishing defectors.
Decentralization and privacy also increase the complexity of the mechanism, requiring users to be more sophisticated, which potentially limits adoption. Balancing legibility with privacy is critical.
The legibility of individuals' preferences and behavior is an asset in some situations. Andrew Critch is a leading researcher in what is known as “transparent” or “open-source” game theory. Here, openness is a design feature where participants can observe and predict other players behavior, which can increase cooperation.
Policy Recommendations
Use Subsidies
Mechanisms that rely on subsidies are the most realistic. Empirically, a significant amount of philanthropic funding exists for public goods. In the U.S. alone, foreign aid spending is $300 billion per year, American citizens spend $500 billion per year on charitable causes, and R&D spending is $660 billion per year. Global philanthropic spending suggests that funding mechanisms can rely on a small amount of altruistic subsidies. It may also be possible to “bootstrap” to larger subsidy levels by using money from one funding round to subsidize a second round of public goods funding.
Quadrants of public goods funding
Deciding on the right public goods funding mechanism depends on the number of different contributors required to support the public good and the size of the subsidy relative to individual contributions.
In practice, situations involving a few, well-resourced actors often lead to the public good being funded without the need for a subsidy. Consider for example international coordination on large research projects such as CERN and cross-industry collaboration in developing EUV lithography. Ostrom has detailed many examples of tight-knit communities solving public goods problems.
However, funding the commons becomes much more difficult as the number of pivotal contributors grows and the subsidy shrinks. Even with a subsidy, the problem of crowdfunding public goods at scale remains unsolved. Though organizations like Gitcoin and Kickstarter have taken important steps towards boosting adoption of their respective mechanisms, we have yet to see a decentralized mechanism that scales to billions of participants.
Such a mechanism would create a new source of public goods funding, one which is far more democratic and accountable than funding from philanthropists or governments. However, all mechanisms may face fundamental constraints on feasibility as the population size grows.
Figure: Informal comparison of how well different public goods funding mechanisms function with varying levels of subsidy and number of contributors.
Some application domains for public goods funding mechanisms
Coordination between large organizations: Governments may coordinate to support large research projects such as CERN, engage in coordinated environmental cleanup, or participate in foreign aid. At the level of government spending, there are no outside funding sources significant enough to subsidize a mechanism. This rules out many mechanisms that depend on subsidies to achieve incentive compatibility. However, since governments interact repeatedly over a multi-decade timeframe, mutual cooperation may arise in the “iterated game”. Assurance contracts are well suited to enable cooperation between governments, their design is simple enough to be used in international treaties, they guarantee coordinated spending, and have an all-pay Nash equilibrium that can be enforced over in a repeated game.
At a smaller scale, corporations and governments may work together to develop a new industry or technology. For example, the development of fracking technology involved coordinated effort from government labs, oil companies, and academia. Government may wish to support R&D in an industry, but faces a principal-agent problem. Corporations may claim they need government support for research they were already planning to do. Some way to extract funding from corporations can make these claims truthful. VCG may work well, as there are relatively few actors with sophisticated knowledge about the value of different projects.
Coordination between government and individuals: If significant subsidies are available, large funding sources can elicit contributions from many individuals. For example, a philanthropist may elicit contributions from many smaller donors by promising to match their donations. In theory, governments can implement a similar scheme and subsidize citizen’s contributions to public goods. Tax deductions for charitable spending are one such system. The properties of such systems are not well studied, it’s possible the subsidy system could be modified to crowdfund many public goods in a manner similar to quadratic funding.
Coordination between individuals: Most public goods funding today comes from individual payments to local and national governments. Therefore, research into improving democratic decision making could improve the provision of public goods.
Smaller organizations tasked with coordinating individual contributions, such as charities, may benefit from simple mechanisms like assurance contracts or lotteries. Groups with more sophisticated users should consider using quadratic voting or the S-process (Lindahl).
Participant Identification and Sybils
Being able to identify and track participants can be important for some mechanisms. For example, quadratic funding and VCG are not immune to Sybil-attacks, so verifying the identity of participants is crucial. Additionally, if funding occurs over many rounds, clearly identifying which individuals are free-riding is critical to punishing defection.
Some mechanisms require no participant identification such as lotteries and some assurance contract implementations.
Project Verification and Management
So far, we have assumed that the providers of public goods actually complete their project. However, crowdfunding services like Kickstarter have been plagued with issues involving fraudulent or unsuccessful projects. Alternatively, some goods may require repeated rounds of funding, and funders may have to consider principal-agent problems when progress cannot be directly observed.
These issues add substantial risk, lowering the value of funding any individual project. Any funding system must take steps to block fraudulent providers. Additionally, some enforcement systems are critical to ensure project completion. One possibility is to withhold a portion of funding until the project meets certain criteria. It is possible that complex contracts or arbitration will be required to properly manage certain projects over a long time horizon.
Mechanisms in the large-population limit
Olson’s book The Logic of Collective Action highlighted the difficulty of collective action in large populations. This applies particularly to the problem of funding public goods. Indeed, Konishi and Shinohara as well as Andreoni showed under different conditions that in the large-population limit, contributions for many mechanisms fall to zero. However, Kocherlakota and Song suggest that a more complicated belief structure combined with ambiguity aversion can make it possible to find a mechanism that funds public goods even at large populations.
On a more positive note, Behringer finds that if citizens have the ability to individually provide a good (as in the provision of open-source software), some mechanisms can still provide the good in a large population.
Bierbrauer and Hellwig show that many mechanisms are implementable as voting systems, with funding raised by taxes. Similarly, Ledyard and Palfrey show that voting schemes can approximate public goods funding schemes. This is consistent with the fact that many mechanisms tend to require increasing subsidies as the number of contributors increases. These results would imply that the most scalable mechanisms are simply voting systems. Unfortunately, these mechanisms are vulnerable to impossibility theorems such as Arrows paradox and the Gibbard–Satterthwaite theorem.
It’s important to determine which mechanisms can work in the large population limit and if any can escape related issues with voting systems. The adjusted mean-thresholding mechanisms of Xi and Xie are promising for public goods with costs that increase slower than the square root of population size. Additionally, new approaches such as quadratic voting, liquid democracy, sortition, and storable votes may avoid Arrow’s paradox in practice. It may also be worth examining voting systems which use money to elicit truthful preferences from voters.
Using Cryptography
While full decentralization brings some benefits, the additional costs and lack of public awareness will limit adoption. Given the existence of altruistic donors in today's public goods funding mechanisms, it is likely that benevolent 3rd parties can be relied upon to run funding mechanisms. A straightforward first step towards reducing trust in these third parties would be to use Zero Knowledge Proofs to prove to each participant that allocations were computed correctly without revealing the other participants preferences.
Conclusion
In general, the study of new public goods funding mechanisms seems to have slowed. Most mechanisms bear similar properties and all of them are constrained by the same impossibility theorems. Mechanisms which satisfy different constraints have already been discovered, and it seems unlikely that a different approach will radically change the landscape. Instead, the bottleneck seems to be in popularizing and scaling existing mechanisms in the real world.
Companies like Kickstarter and Gitcoin have been successful at popularizing certain aspects of crowdfunding, but neither has achieved the scale required for citizens to provide global public goods without resorting to international treaty. In the large population limit, crowdfunding in its current form may be infeasible.
To escape these limitations, theoretical research will need to relax some of the standard assumptions in mechanism design, considering the effect of altruism, the complexity of manipulation, and the importance of reputation in funding mechanisms. In the real world, there is exciting work ahead in terms of lowering real world costs, experimenting with different approaches and increasing awareness. A popular, secure and robust crowdfunding mechanism could create a world where billions of people can coordinate for the greater good.
Acknowledgements
Thank you to Rubi J. Hudson, Matthew W. Thomas, Joel Miller, and Kris Gulati for feedback on this report.
Appendices
Appendix 1: useful mechanism properties
Pareto Efficiency: The outcome achieved by the mechanism maximizes the overall welfare or some other desirable objective function.
Incentive Compatibility: Designing mechanisms so that participants are motivated to act truthfully, without gaining by misrepresenting their preferences.
Individual Rationality: Ensuring that every participant has a non-negative utility (or at least no worse off) by participating in the mechanism.
Budget Balance: The mechanism generates sufficient revenue to cover its costs or payouts, without running a deficit.
Coalition-Proofness: Preventing groups of participants from conspiring to manipulate the mechanism to their advantage.
Appendix 2: Links to Additional Mechanisms
A more comprehensive list of references relevant to public goods funding mechanisms can be found here and in the links below:
Liberal Radicalism: A Flexible Design For Philanthropic Matching Funds
Optimal Allocation of Public Goods: A Solution to the “Free Rider” Problem
The MDP Procedure for public goods and local strategy proofness
An Efficient Tˆatonnement Process for the Public Good Problem
Funding Public Projects: A Case for the Nash Product Rule
Limited-Tenure Concessions for Collective Goods
Electronic Commerce and the Street Performer Protocol
A Minimum Contribution Mechanism for the Provision of Public Goods
A Budget-balanced, Incentive-compatible Scheme for Social Choice
An Efficient Dynamic Mechanism
A Simple Incentive Compatible Scheme for Attaining Lindahl Allocations
Domain expansion of the pivotal mechanism
Public Good Provision with No Extortion
The Conditional Contribution Mechanism for the Provision of Public Goods
The private provision of public goods via dominant assurance contracts
Dominant Assurance Contracts with Continuous Pledges
Financing Public Goods by Means of Lotteries
Hybrid lotteries for financing public goods
Public-Good Provision in Large Economies
Providing public goods in two steps
Strength in Numbers: Robust Mechanisms for Public Goods with Many Agents
Two-Part Tariff Lottery: A Means to Provide Public Good at the Social Optimum
Using Tontines to Finance Public Goods
A Practical Quantum Mechanism for the Public Goods Game
Comparing Crowdfunding Mechanisms: Introducing the Generalized Moulin-Shenker Mechanism
Welfare Undominated Groves Mechanisms
Optimal mechanism design for the private supply of a public good
A Nonparametric, Efficient Public Good Decision Mechanism: Undominated Bayesian Implementation
Robust Mechanisms for the Financing of Public Goods
The Provision of a Public Good with a direct Provision Technology and a Large Number of Agents
The provision point mechanism with refund bonuses
Appendix 3: Experimental Public Goods Games
Sustaining cooperation in laboratory public goods experiments: a selective survey of the literature
Incentive-compatible Mechanisms for Pure Public Goods: A Survey of Experimental Research
Funding public goods with lotteries: experimental evidence
Learning dynamics for mechanism design: An experimental comparison of public goods mechanisms
Appendix 4: More desiderata for designing mechanisms
Below we list some useful features and if applicable, suggest which techniques may be able to serve this role. We ignore basic financial and communications infrastructure such as contracts, secure payments, loans, escrow accounts, and secure messaging.
Private and public randomness: Some mechanisms require randomness for differential privacy or collusion resistance. Public randomness beacons or verifiable random functions might serve this purpose.
Various forms of identity: To prevent sybil attacks, some form of identity is needed. If reputation is important, a public identity is preferred. If anonymity is required, zero-knowledge proofs or re-randomizable encryption may be necessary.
Reputation systems: Reputation is an important incentive to fund public goods. Some form of reputation score or record of participation can be useful for repeated games. These scores can help identify bad actors or help communities coalesce around a particular funding venue.
Badges of spending: Some mechanisms benefit from the reputational effects of providing for public goods. In that case, public certifications of spending attached to a personal ID would be valuable.
Provable participation: Even if spending should be kept private, users may want to prove their participation in a funding mechanism in order to boost their reputation or as part of an agreement.
Verifying Non-pecuniary Actions: Though not all users may be able to provide much funding for a good, they may be able to volunteer their time, labor, or advocacy. If these activities can be verified, mutual commitments of time and money can be made amongst users. Enforcing these actions may require financial penalties and reduced reputation scores.
Hidden mechanisms: Concealing which mechanism is being used can prevent dishonest behavior and reduce information leakage. Zero-knowledge mechanisms have a straightforward application here.
Verifiable Mechanisms: Users may want certain guarantees about a mechanism before or after participation, especially if the mechanism being used is concealed. Ex-ante, they may want to upper-bound their amount of spending towards the good, ex-post, they may require proof that a sufficient number of individuals contributed.
Private Computation: Ideally, individuals could privately compute allocations without revealing their preferences to another party. MPC may be suitable for this.
Verifiable computation: Regardless of how allocations are computed, users would benefit from some assurance that they were computed correctly. ZKP may be suitable for this.
Anti-collusion infrastructure: Like secure voting systems, there is a threat of buying votes in a funding mechanism. Collusion can be discouraged by making it impossible for users to prove how they reported their preferences. This infrastructure must be extended to prevent collusion between the 3rd party and the users.
Secure voting: In the large population limit, many mechanisms begin to resemble voting systems. Infrastructure for secure, decentralized voting has substantial overlap with 1-round public goods funding mechanisms.
Management of Public Goods Providers: To keep providers accountable, checks must be in place to ensure the funding is spent appropriately. Users will need ways to verify spending, monitor provider activities, punish non-compliance, and adjudicate ambiguous situations.
Bootstrapping Funding Systems: Bootstrapping public goods funding systems where the revenue from one round is used as the subsidy for a subsequent round can require storing and distributing funds over multiple iterations This may require a new system that stores the collected contributions and performs a subsequent fundraising round. For example, a small group of philanthropists could gather a pot of money using an assurance contract, and then use that pot as the prize in a charitable lottery. This process is relatively straightforward under a legal system, but it may be useful to implement using a cryptographic scheme.
Conditioning on future events: Management of public goods providers can be performed if funding commitments are conditional on future events. For example, a provider could be paid only after users verify that a public park has been built. This requires holding funds in escrow, loaning startup funds to providers, and using trusted judges or prediction markets to provide a “ground truth”.
Multi-round Mechanisms: Repeating mechanisms over multiple rounds with the same participants can change the dynamics dramatically. In general, adding multiple rounds tends to increase coordination among participants, since defectors can be punished in future rounds. This is illustrated by the folk theorems, where adding many rounds to a game adds many new Nash equilibria beyond the one-shot game. These kinds of cooperative dynamics can be observed in tight-knit communities, and are the focus of Ostrom’s Nobel-prize winning work.